The formula given in my book does not seem to work in Mathcad Prime 30 In the book there is no multiplier (*) printed after tan^2 and cos^2 There is just empty space I did change the formula around in all kinds of ways I put tan inside parenthesis like (tan)^2, or (tan^2* (gammaQ)), or (tan (gammaQ)^2) but nothing worksSome common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x = 3 sin x – 4 sin³x 5) cos3x = 4 cos³x – 3 cosxThe Pythagorean formula for tangents and secants There's also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it's unnecessary Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas
1
Tan 2x all formula
Tan 2x all formula-All Trigonometry Formulas List Most Trigonometry formulas revolve around ratios and extremely handy to solve complex problems in Trigonometry If you want to appear for any competitive exams after your school then handson knowledge of different Trigonometry formulas is essential The basic of any Trigonometry formula is a Trigonometry Identity There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com
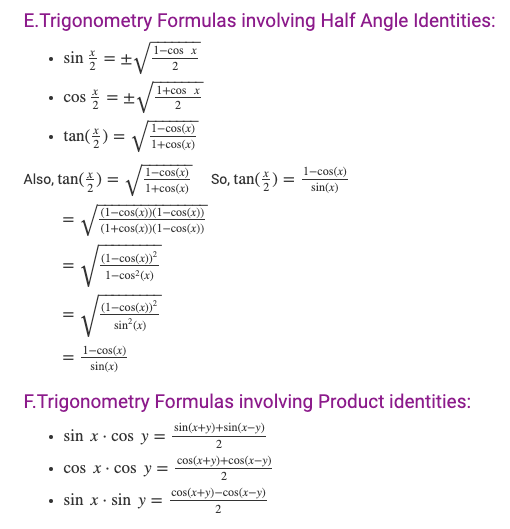
The period of the tan(2x) tan (2 x) function is π 2 π 2 so values will repeat every π 2 π 2 radians in both directions x = π 8 πn 2, 5π 8 πn 2 x = π 8 π n 2, 5 π 8 π n 2, for any integer n nSolve for x tan(2x)tan(x)=1 Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Replace with in the formula for period Solve the equation Tap for more steps The absolute value is the distance between a number and zero TheTan 2 θ = sec 2 θ − 1 The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula
One can show using simple geometry that t = tan (φ/2) The equation for the drawn line is y = (1 x)t The equation for the intersection of the line and circle is then a quadratic equation involving t The two solutions to this equation are (−1, 0) and (cos φ, sin φ)Therefore, tan 60° = \(\frac{2 tan 30°}{1 tan^{2} 30°}\) (ii) The above formula is also known as double angle formulae for tan 2A Now, we will apply the formula of multiple angle of tan 2A in terms of A or tan 2A in terms of tan A to solve the below problem 1 Express tan 4A in terms of tan A Solution tan 4a = tan (2 ∙ 2A)Precalculus Trigonometric Functions A trigonometric equation is any equation that includes a trigonometric function There are two basic types of trigonometric equations identities and conditional equations Identities are equations that hold for any angle Conditional equations are equations that are solved only by certain angles
Trigonometric Equation Calculator \square! Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer linkFORMULAS TO KNOW Some trig identities sin2xcos2x = 1 tan2x1 = sec2x sin 2x = 2 sin x cos x cos 2x = 2 cos2x 1 tan x = sin x cos x sec x = 1 cos x cot x = cos x sin x csc x = 1 sin x Some integration formulas R xn dx = xn1 n1 C R 1 x dx = lnjxjC R




Double Angle Identities Trigonometry Socratic




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Powerpoint
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 xBASIC ANTIDERIVATIVE FORMULAS YOU REALLY NEED TO KNOW !!



Solution Determine The Period Of Y Tan 2x




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com
Find the exact value of `cos 2x` if `sin x= 12/13` (in Quadrant III) Answer Using the following form of the cosine of a double angle formula, cos 2 α = 1− 2sin 2 α , we have1 tan2 Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radians then ˇ 180 = t x) t= ˇx 180 and x= 180 t ˇ Half Angle Formulas sin = r 1 cos(2 ) 2 cos = r 1 cos(2 ) 2 tan = s 1 cos(2 ) 1 cos(2 ) Sum and Di erence Formulas sin( ) = sin cos cos sin cos( ) = cos cos sin sin tan( ) = tan tan 1 tan tan Product toTrigonometric function of sin 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, sin 2A = 2 sin A cos A ⇒ sin 2A = 2 s i n A c o s A ∙ cos 2 A ⇒ sin 2A = 2 tan A ∙ 1 s e c 2 A ⇒ sin 2A = 2 t a n A 1 t a n 2 A There for sin 2A = 2 t a n A 1 t a n 2 A




Trigonometric Integrals Geogebra



Trigonometric Functions With Their Formulas
Ex dx = ex C ax dx = ax lna C 1 x dx =lnx C cosxdx=sinxC sec2 xdx=tanxC sinxdx= −cosx C csc2 xdx= −cotx C secxtanxdx=secx C 1 1x2 dx =arctanxC 1 √ 1− x2 dx =arcsinxC cscxcotxdx= −cscx C secxdx=lnsecxtanx C cscxdx= −lncscxcotx C xn dx = xn1 n1 C, when n = −1 Here areTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `tan 3xtan 2xtan x= tan 3x tan 2x tan x ` We solve this using a specific method First we write px q = A (d (√ (ax 2 bx c))/dx) B Then we find A and B Our equation becomes two seperate identities and then we solve Some examples are (x 3) √ ( 3 4x x 2 ) View solution x √ (1 x x 2 ) dx – View Solution Check Practice Questions
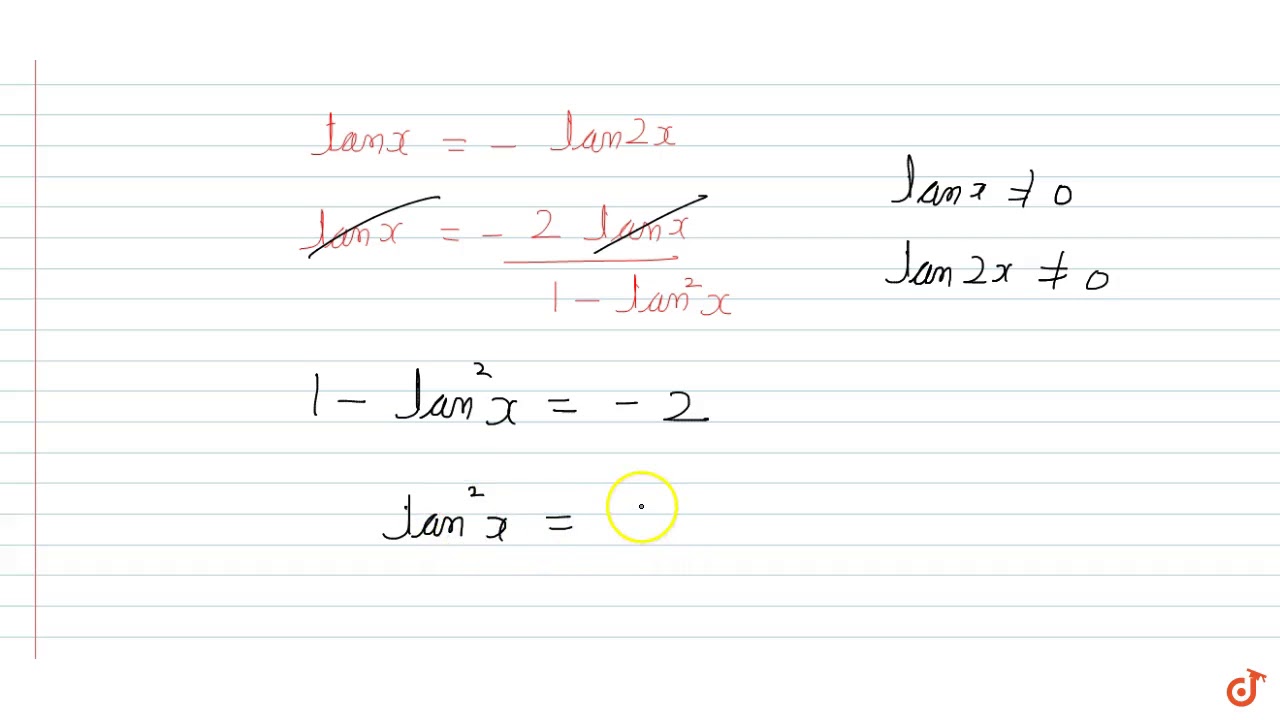



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube




In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)Write tan(3x) as tan(2x x) and then use the expression above to write tan(3x) in terms of tan(x) and tan(2x) Next write tan(2x) as tan(x x) and use the expression above again to write tan(3x) in terms of tan(x) Simplify the expression Harley1 cot 2 x = cosec 2 x;




14 2 Trigonometric Identities



1
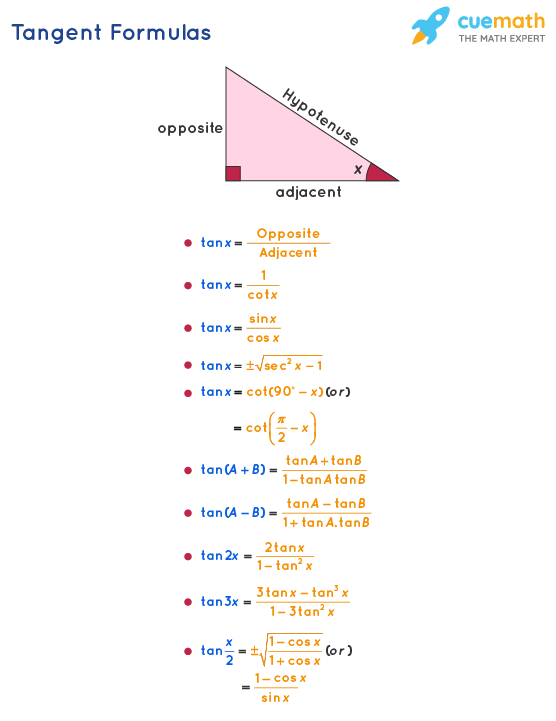
Tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function sinq, q can be any angle cosq, q can be any angle tanq, 1,0,1,2, 2 qpnnIn trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per Class 10, 11 and 12 syllabi Also, find the downloadable PDF of trigonometric formulas at BYJU'SWe urge all the scholars to understand these formulas and then easily apply them to solve the various types of Trigonometry problems Trig Indentity Cos Pythagorean Identities Radians Sin Tan repeat after 2𝛑 Trigonometry Basic Formula




Tan 2x Formula What Is Tan 2x Formula Examples



1
From this formula we can derive tan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formula 8K views View upvotes 9 6 Related Questions More Answers Below What is the formula of cosec(AB)?Plot of the six trigonometric functions, the unit circle, and a line for the angle = radians The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the axis, while Cos(θ), 1, and Cot(θ) are lengths along the axis starting from the originLearn formula of tan(2x) or tan(2A) or tan(2θ) or tan(2α) identity with introduction and geometric proof to expand or simplify tan of double angle




Double Angle Identities Solutions Examples Videos Worksheets Games Activities




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic
Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and General solution of tan(2x)tan(x) = 1 For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as ( 2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = ( 2n 1) π 2 But the book solved using the formula of tan(2x), and got the solution as ( 6n ± 1) π 6 I can see that my solution has oddIntegral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integral of sin(x), integ




General Solution Of Tan 2x 3 Sqrt 3 Is




Tangent Half Angle Formula Wikipedia
1 tan 2 x = sec 2 x; You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the Formula




Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id




Prove The Identity 3 Tan 3x 9 Tan X 3 Tanx 13 Chegg Com
Tan2x Formula Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved exampleAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsHere is the Integration Formulas List The formula list is divided into below sections a Basic integration formulas bIntegration formulas for Trigonometric Functions



Prove The Identity 3 Tan 3x 9 Tan 3 Tanx 1 3 Tan Chegg Com




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unit Integration Formulas If you are looking for Integration Formulas then you have landed on the right page Here we will provide you with all the formulas for integration that will help you in your school as well as board exams Since there is no short trick to remember or learn these formulas, all you have to do is practice questions and implement these formulasDOUBLEANGLE, POWERREDUCING, AND HALFANGLE FORMULAS tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first




Tan2x ただの悪魔の画像




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Cosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosineYou just have to click on the topic and get all relevant details and formulas with simple navigation Also, we have discussed the applications of the different mathematical concepts in real life and how it can help students in their careers Well, formulas can be simpler or complex based onTan (2 x) = 2 For example, sin (2 x) = sin (x x) = sin x cos x cos x sin x = 2 sin x cos x The formula for cosine follows similarly, and the formula tangent is derived by taking the ratio of sine to cosine, as always The double angle identities can also be derived from the de
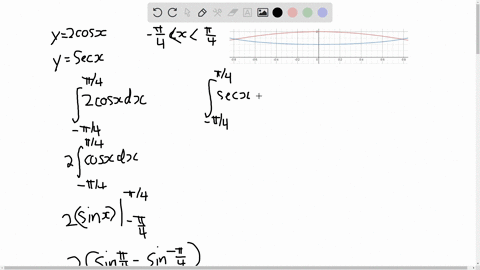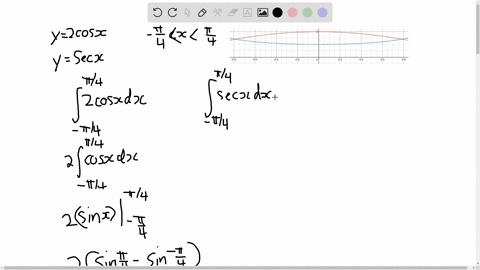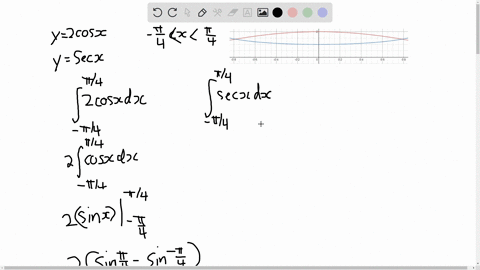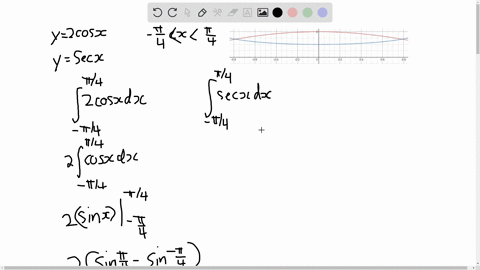



Solved Find The Area Of The Region Bounded By The Given Curves Y Tan X Y Tan 2 X 0 Le X Le Frac Pi 4
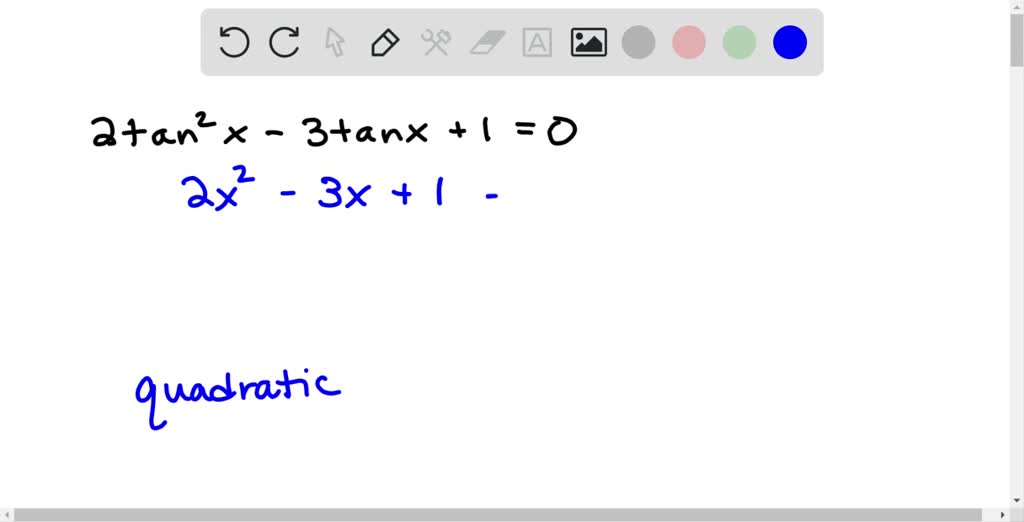



Solved The Equation 2 Tan 2 X 3 Tan X 1 0 Is A Trigonometric Equation That Is Of Type
Welcome to Omni's halfangle calculator, where we'll study halfangle trig identitiesThe double angle formulas let us easily find the functions of twice the angle Here, we'd like to do the same, but instead of multiplying the angle by two, we'll divide itIn fact, the main tool to find the sin, cos, and tan halfangle formulas are the power reducing identities
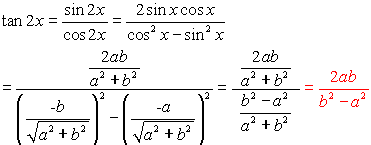



Six Trigonometric Functions Mathbitsnotebook Ccss Math



Find The General Solution For The Equation Sec 2 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Lesson 4 5 Double Angle Formulas




Power Reducing Formulas And How To Use Them With Examples Owlcation



What Is The Formula Of Tan2x Quora




Integrate Sec 2x Method 2




Ch 5 5 Multiple Angle And Product To Sum Formulas Ppt Download Free Math Help Trigonometry Math Review Worksheets




Integrate Tan 2x




Weierstrass Substitution Wikipedia



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau



Www Mayfieldschools Org Downloads 4 8 double angle formulas answers Pdf




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55




Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com




The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is Youtube




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help




Differentiate The Following From First Principle Tan 2x



Elementary Calculus Theorem 1
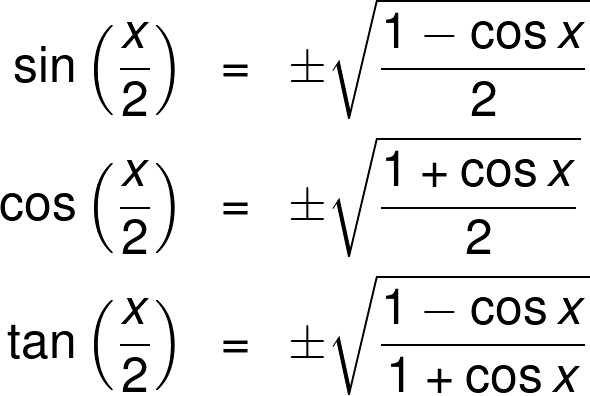



Half Angle Calculator



Ilectureonline
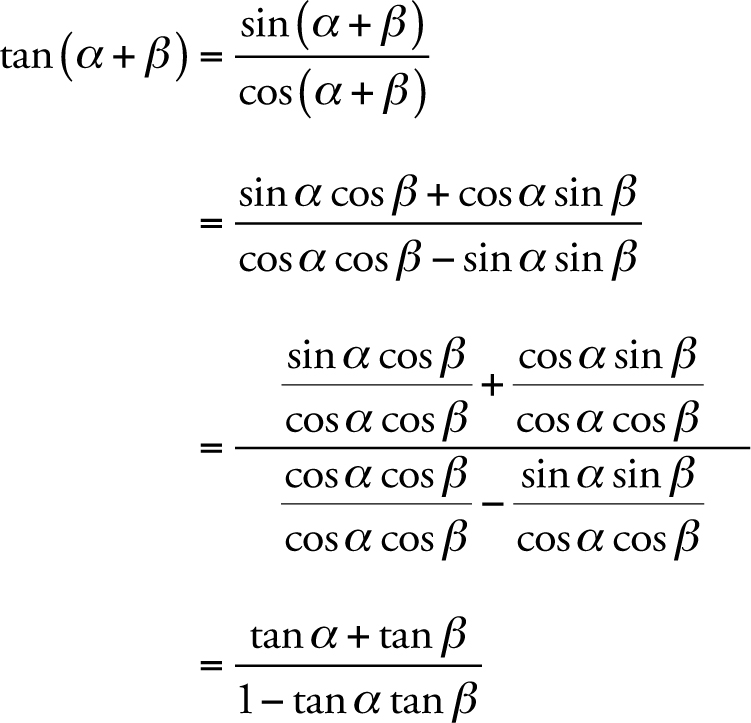



Tangent Identities




Find Sin 2x Cos 2x And Tan 2x If If Tan X 2 And Gauthmath




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help




How To Graph Tan Ex Y Tan2x Study Com




Integrate Tan 2x By Parts
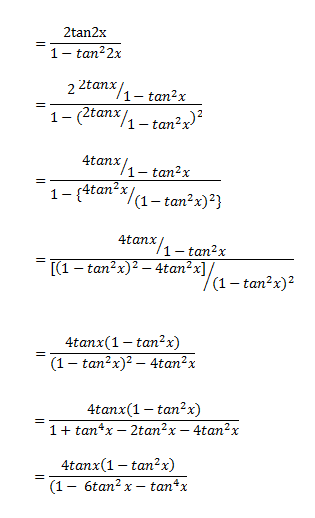



Trigonometry Functions Class Xi Exercise 3 3 Breath Math
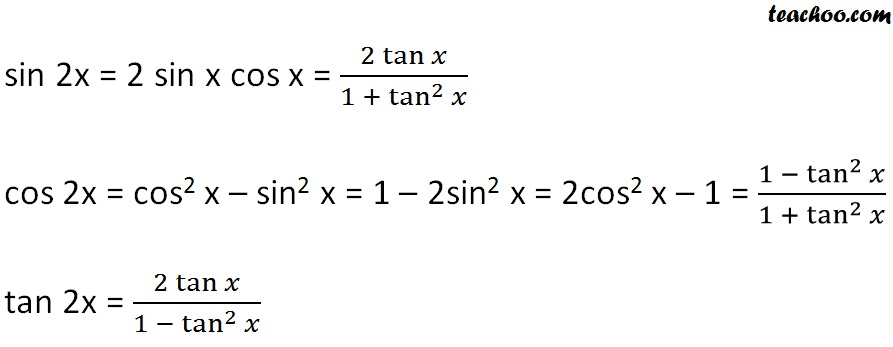



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
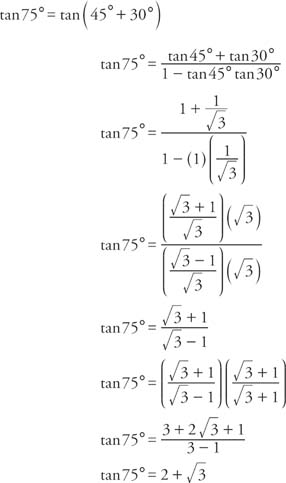



Tangent Identities




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



bestpictjcry Tan 2x Tan 2x




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




Sin2x Cos2x 1 Proof




Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com
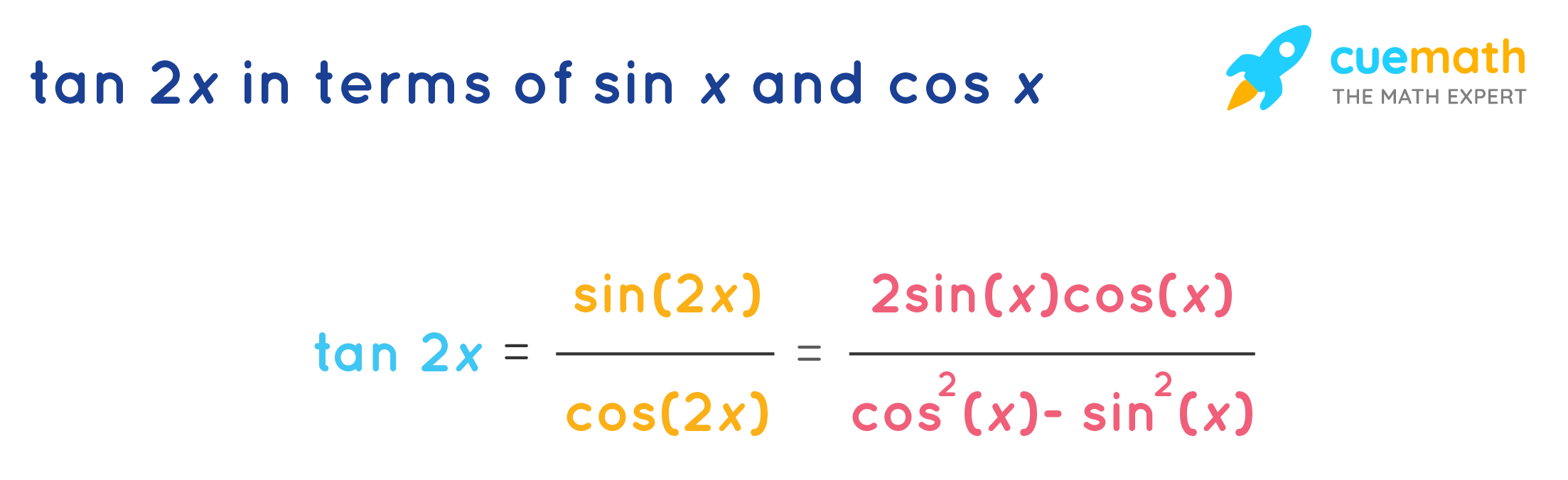



Tan 2x Formula What Is Tan 2x Formula Examples




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com



Differentiate The Following W R T X Tan 1 3 2x 1 6x Maths Pyranic




Multiple Angle Formulas Overview Video Trigonometry Ck 12 Foundation




What Is Integral Of Sin2x Tan2x Quora




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com



Tangent Formula What Are Tangent Formulas Examples



Establish The Given Limit Formula Stumbling Robot




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1
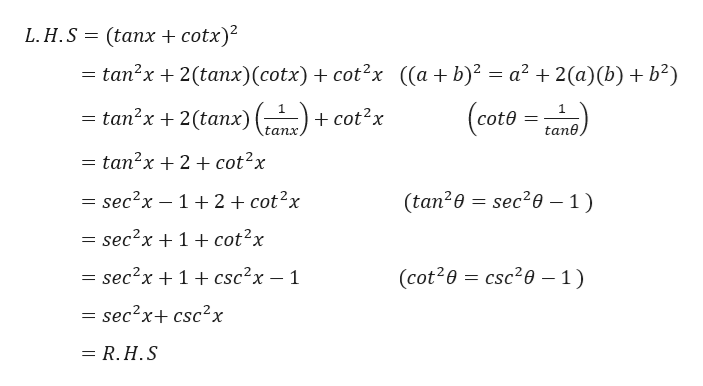



Answered The Question Says To Confirm That The Bartleby




1 Sin 2 X Formula Sepertikisahku




Art Of Problem Solving




Solve The Equation Tan 2x Cot X Pi 6




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P



Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Tangent Half Angle Formula Wikipedia




Quiz Worksheet Double Angle Formula Study Com



Solved Givencos 3 0 5 Findtan2 6 Use The Formulatan2x 1 Cos2x 1 Cos2x Course Hero
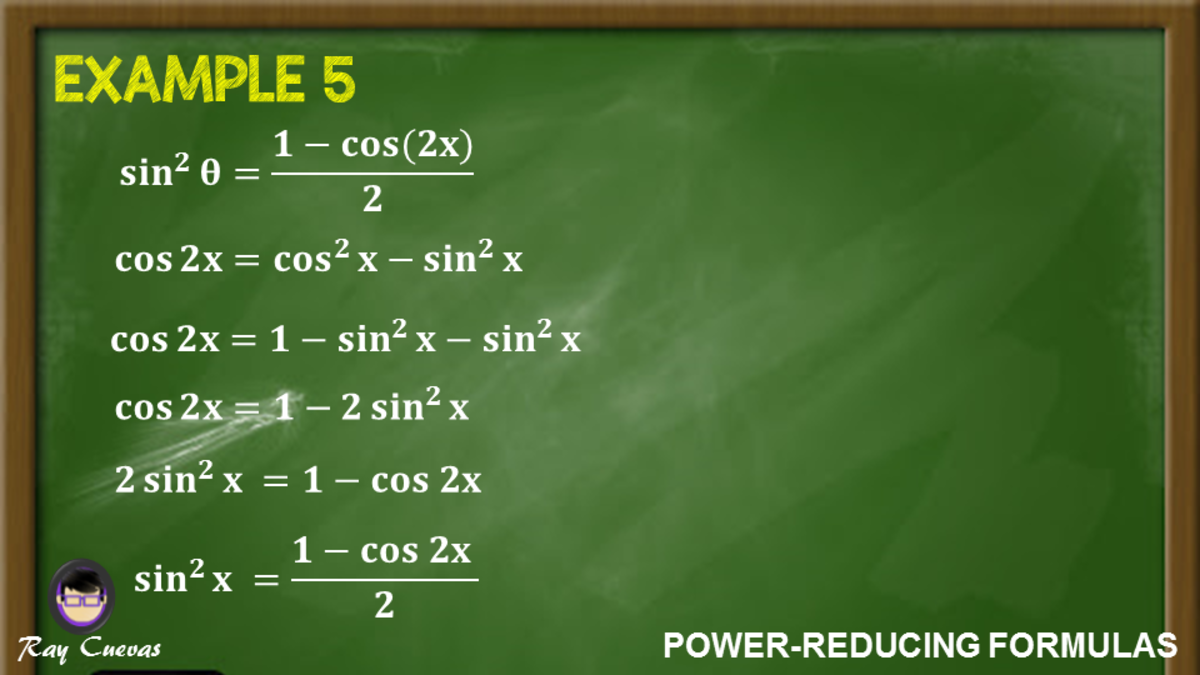



Power Reducing Formulas And How To Use Them With Examples Owlcation




Weierstrass Substitution Wikipedia




Trig Identity Sec2x Minus Tan2x T10 Youtube



What Are The Formulas Of Sin 2x Quora



Ilectureonline




Math34 Trigonometric Formulas



Points Or No Points Maths Sl Ib Survival
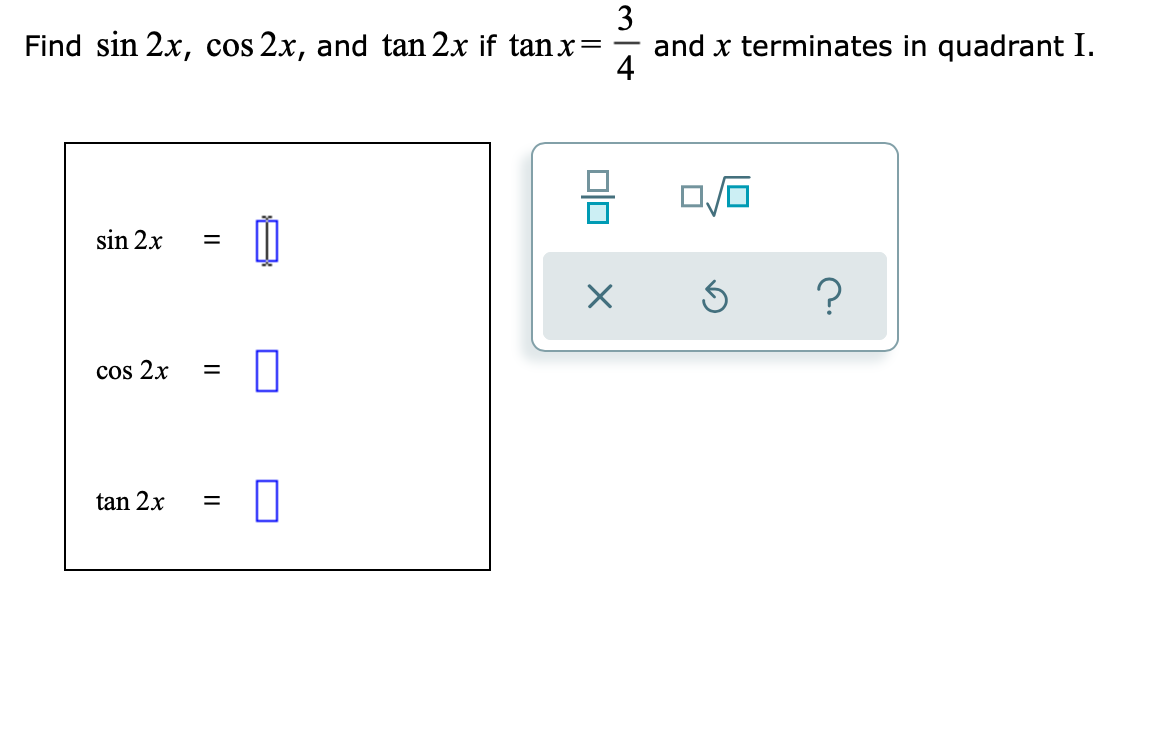



Answered 3 And X Terminates In Quadrant I 4 Bartleby



1




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download




Power Reducing Calculator




Math34 Trigonometric Formulas




Sum And Difference Identities Video Lessons Examples And Solutions




Section 7 3 Double Angle Half Angle And Chegg Com




Double Angles Ppt Video Online Download



What Are The Formulas Of Cos 2x Quora
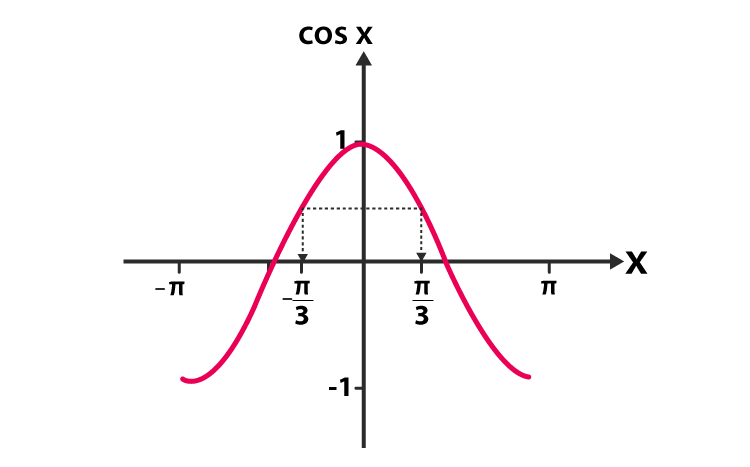



Sin 2x Formula Sin 2theta Formula Practice Examples




Using Double Angle Formulas Objective To Apply The Double Angle



Trig Identities Hsn Forum




Section 7 3 Double Angle Half Angle And Sum



0 件のコメント:
コメントを投稿